Lease Square Fit
- Maximum likilihood
Least Square Fit to a Straight Line
Central limit Theorem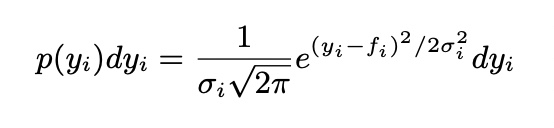
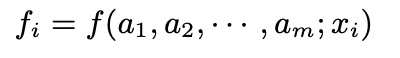
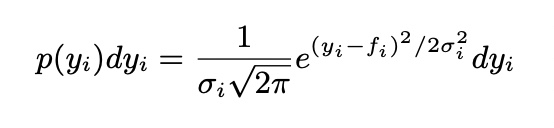
평균과 분산이 발산하지 않는 경우, 랜덤하게 뽑은 변수는 가우시안 분포에 근사함
Maximum likelihood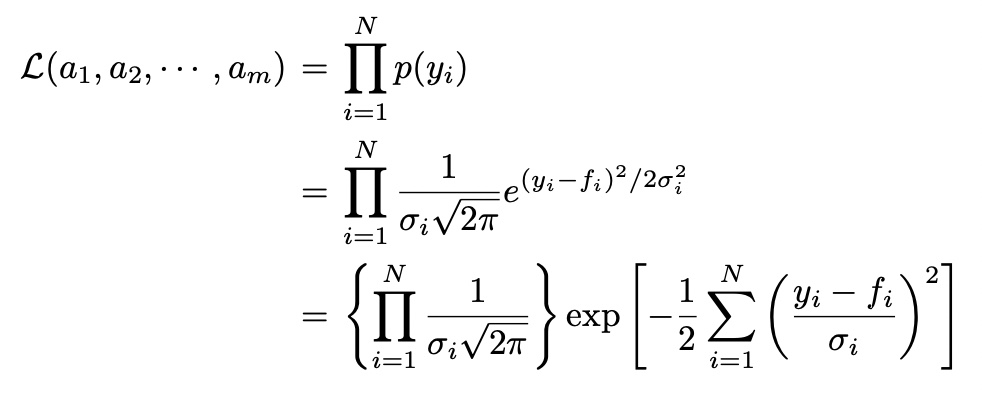
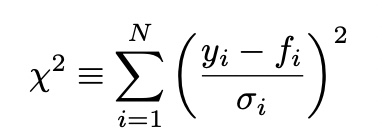minimize chi-squared->maximize likelihood
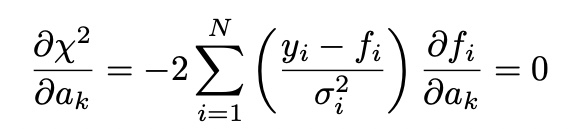
(둘 째 줄 a 계수 오차(*x_i))
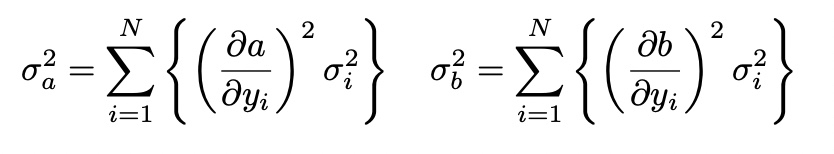
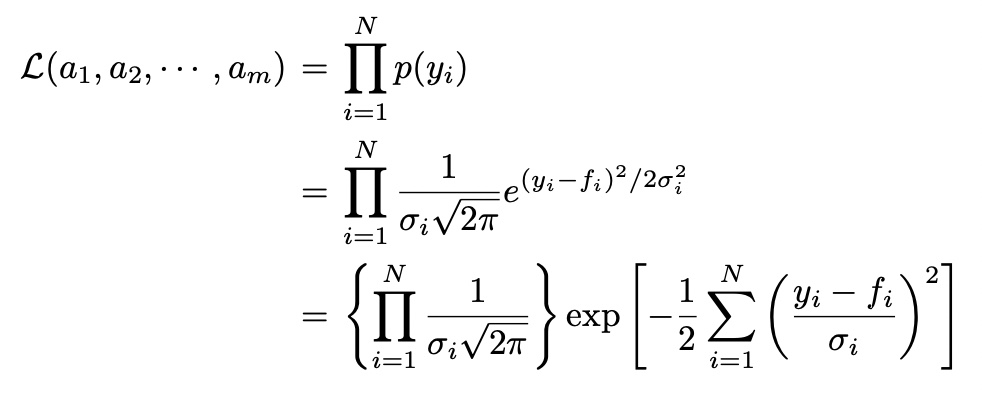
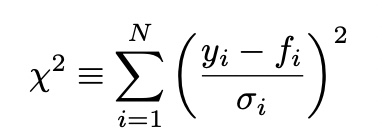minimize chi-squared->maximize likelihoodthen,
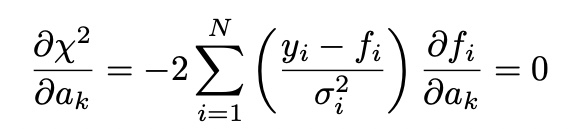
선형 LSE fitting
then, f(x)=a+bx
(둘 째 줄 a 계수 오차(*x_i))with matrix form
Errors
Error propagation:
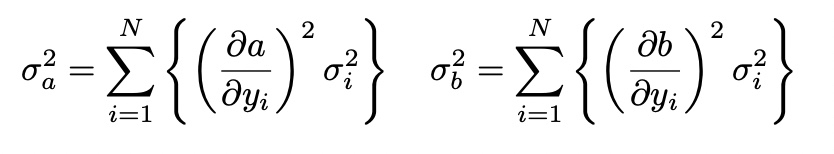
then,
# linear fitting
import numpy as np
import matplotlib.pyplot as plt
import random as rd
x=np.array(range(1, 10), float)
y=np.array(x*5+4, float)
for i in range(len(y)):
y[i]+=rd.random()-0.5+0.1
sigma=np.ones_like(x)
alpha=np.sum(1/sigma**2)
beta=np.sum(x/sigma**2)
gamma=beta
delta=np.sum(x**2/sigma**2)
theta=np.sum(y/sigma**2)
phi=np.sum(x*y/sigma**2)
D=alpha*delta-beta*gamma
a=(theta*delta-beta*phi)/D
b=(alpha*phi-gamma*theta)/D
###
yy=a+x*b
plt.plot(x, y)
plt.plot(x, yy)
plt.show()
# error
delta_a=delta/D
delta_b=alpha/D
print("a= ", a, " +/- ", delta_a, sep="")
print("b= ", b, " +/- ", delta_b, sep="")
Gradient Descent
Newton-Raphson이랑 살짝 다름
# J=(y-y_hat)^2/sigma
import numpy as np
import matplotlib.pyplot as plt
import random as rd
x=np.array(range(1, 10), float)
y=np.array(x*5+4, float)
for i in range(len(y)):
y[i]+=rd.random()-0.5+0.1
a=rd.random()
b=rd.random()
alpha=0.0001
h=1e-3
tolerence=1e-8
print("initial state\na: ", a, "b: ", b, sep="")
def reg(a, b):
global x
return a+b*x
def d_chi_sq(f, a, b, sigma=1.):
global y
return np.sum(((y-f(a, b))/sigma)**2)
dc_da=1; dc_db=1
while(abs(dc_da)>tolerence or abs(dc_db)>tolerence):
dc_da=(d_chi_sq(reg, a+h, b, sigma=1.)-d_chi_sq(reg, a-h, b, sigma=1.))/(2*h)
dc_db=(d_chi_sq(reg, a, b+h, sigma=1.)-d_chi_sq(reg, a, b-h, sigma=1.))/(2*h)
a-=alpha*dc_da
b-=alpha*dc_db
print("after DG\na: ", a, " b: ", b, sep="")
plt.plot(x, y, 'ro')
yy=a+b*x
plt.plot(x, yy)
plt.show()